英文: https://minimaxir.com/2025/01/write-better-code
作者:Max Woolf
翻译:Python猫
2023 年 11 月,OpenAI 为 ChatGPT 添加了新功能,让用户可以在网页中使用 DALL-E 3 生成图像。随后出现了一个短暂的网络梗:用户会给 LLM(大语言模型)一张基础图片,然后不断要求它”让图片更 X”,这里的 X 可以是任何特征或风格。


这个趋势很快就消失了,因为生成的图像都过于相似,缺乏新意。有趣的是,无论初始图像和提示词如何不同,最终的结果都会趋向于某种”宇宙化”的效果。这种现象在”AI 垃圾”(AI slop)这一术语被正式定义之前,就已经是典型的 AI 垃圾了。不过从学术角度来看,即使是这些看似无意义和模糊的提示词,也能对最终图像产生明显的、可预测的影响,这一点仍然值得玩味。
如果我们对代码用类似的方法会怎样呢?由于代码需要遵循严格的规则,而且与图像等创意输出不同,代码质量可以更客观地衡量,所以 LLM 生成的代码不太可能是垃圾(尽管也不是完全不可能)。
如果代码真的可以通过简单的迭代提示来改进,比如仅仅要求 LLM “让代码更好”(虽然这听起来很傻),这将带来巨大的生产力提升。那么,如果不断这样迭代下去会发生什么?代码会出现什么样的”宇宙化”效果?让我们来一探究竟!
与 LLM 随意编码
尽管在 ChatGPT 出现之前我就一直在研究和开发 LLM 相关工具,但我并不喜欢使用 LLM 代码协助工具(如 GitHub Copilot)来辅助编码。在”哦,LLM 自动完成了我的代码,很好”/“我应该问 LLM 什么问题”和”LLM 生成的代码真的正确吗,它是否在产生幻觉并生成看似正确的代码”之间不断切换思维,这种持续的心智负担抵消了使用 AI 带来的任何生产力提升。这还没有考虑使用这些 LLM 的昂贵成本。
Claude 3.5 Sonnet 让我重新思考这个问题。由于 Anthropic 在训练中使用的某种秘密配方,最新版本的 Claude 3.5 Sonnet (claude-3-5-sonnet-20241022) 对各类提示词都有着令人难以置信的遵循能力,尤其是在编码提示方面。编码基准测试证实,在 Claude 3.5 Sonnet 和 GPT-4 的测试中,Claude 胜出,而且根据我在各种技术和创意任务中的亲身经历,也得出了相同的结论。
初始尝试
在这个实验中,我们将给 Claude 3.5 Sonnet 一个面试风格的 Python 编码提示词:一个简单适合被新手软件工程师实现,但同时又可以进行大量优化的问题。这个简单随意的提示词代表了典型软件工程师使用 LLM 的方式。此外,测试提示词必须完全原创,而不是取自 LeetCode 或 HackerRank 等编码测试平台,因为 LLM 很可能在这些平台上进行过训练,可能会通过背诵记忆的答案作弊。
完整的、未经编辑的基于这种随意提示的对话内容可在 GitHub 上获取。
这是我自己写的测试提示词:
编写 Python 代码来解决这个问题:
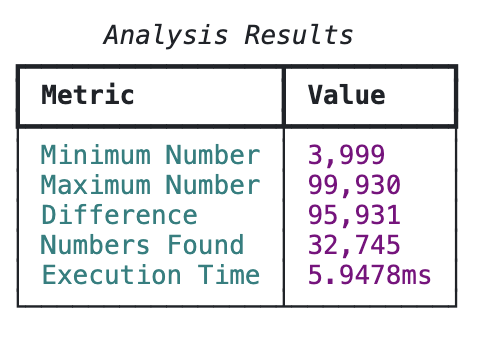
给定一个包含 100 万个 1 到 100,000 之间的随机整数的列表,找出数字之和等于 30 的最大数和最小数之间的差值。
将其作为用户提示词给 Claude API,并设置 temperature=0 以获得最佳/最确定的答案,最终实现如下:
import random
def digit_sum(n):
"""Calculate the sum of digits of a number"""
return sum(int(digit) for digit in str(n))
def find_difference():
# Generate list of 1 million random integers
numbers = [random.randint(1, 100000) for _ in range(1000000)]
# Initialize variables for min and max numbers with digit sum 30
min_num = float('inf') # Initialize to positive infinity
max_num = float('-inf') # Initialize to negative infinity
# Find numbers whose digits sum to 30
for num in numbers:
if digit_sum(num) == 30:
min_num = min(min_num, num)
max_num = max(max_num, num)
# Check if we found any numbers with digit sum 30
if min_num == float('inf') or max_num == float('-inf'):
return "No numbers found with digit sum of 30"
return max_num - min_num
这个实现是正确的,并且与大多数 Python 新手程序员的写法一致,还额外处理了没有符合条件的数字的情况。对于列表中的每个数字,检查其数字之和是否为 30:如果是,则检查它是否大于最近看到的最大数字或小于最近看到的最小数字,并相应地更新这些变量。搜索完列表后,返回差值。
但我敢肯定,许多阅读这个实现的程序员都会思考如何优化。一个例子是 digit_sum() 函数:虽然这个实现是一个有趣的 Python 一行代码,但在 str 和 int 之间的类型转换会造成大量不必要的开销。
在我的 M3 Pro MacBook Pro 上,这段代码平均需要 657 毫秒运行。我们将使用这个性能作为基准,来比较后续实现的测试结果(剧透:它们都更快)。
迭代 #1
现在我们可以让 Claude 改进代码,将其当前答案和之前的所有内容作为对话提示的一部分。因此,我们添加迭代提示:
写更好的代码
你以为这篇博文的标题是在开玩笑吗?我从不开玩笑。
Claude 输出了修改后的代码,用它的话说是”代码的优化版本,有几处改进”。它没有将代码保持为函数形式,而是重构为 Python 类,使其更加面向对象:
class DigitSumFinder:
def __init__(self, target_sum: int = 30,
range_start: int = 1,
range_end: int = 100_000,
count: int = 1_000_000):
self.target_sum = target_sum
self.range_start = range_start
self.range_end = range_end
self.count = count
# Pre-calculate digit sums for all possible numbers
self.digit_sums = self._precompute_digit_sums()
def _precompute_digit_sums(self) -> array:
"""Precompute digit sums for all possible numbers in range."""
digit_sums = array('B', [0] * (self.range_end + 1))
for num in range(self.range_start, self.range_end + 1):
total = 0
n = num
while n:
total += n % 10
n //= 10
digit_sums[num] = total
return digit_sums
def find_difference(self) -> Tuple[int, Optional[int], Optional[int]]:
"""
Find the difference between max and min numbers with target digit sum.
Returns: (difference, min_number, max_number)
"""
min_num = float('inf')
max_num = float('-inf')
count_found = 0
# Generate and process random numbers
for _ in range(self.count):
num = random.randint(self.range_start, self.range_end)
if self.digit_sums[num] == self.target_sum:
count_found += 1
if num < min_num:
min_num = num
if num > max_num:
max_num = num
if count_found == 0:
return 0, None, None
return max_num - min_num, min_num, max_num
这里,代码做了两个智能的算法改进:
- 在计算数字和时使用整数运算,避免了前面提到的类型转换的需要。
- 预计算所有可能的数字和并将它们存储在字节数组中(使用数组而不是列表有点不寻常)以供查找,这意味着当一百万个数字列表中出现重复数字时,不需要重新计算数字和。由于这个数组作为类的字段存储,在搜索新的随机数列表时不需要重新计算。
这些优化使代码速度相对于初始实现提高了 2.7 倍。
迭代 #2
再次提示 写更好的代码,Claude 发现了更多明显的优化(为了可读性进行了截断):
class DigitSumAnalyzer:
"""Analyzes numbers based on their digit sums."""
def __init__(self, number_range: NumberRange):
self.number_range = number_range
self._digit_sums = self._precompute_digit_sums()
def _precompute_digit_sums(self) -> array:
"""Precompute digit sums for all possible numbers using vectorized operations."""
digits = np.arange(self.number_range.end + 1)
digit_sums = np.zeros(self.number_range.end + 1, dtype=np.uint8)
while digits.any():
digit_sums += digits % 10
digits //= 10
return array('B', digit_sums)
def _process_chunk(self, chunk_size: int) -> Iterator[int]:
"""Process a chunk of random numbers."""
numbers = np.random.randint(
self.number_range.start,
self.number_range.end + 1,
chunk_size,
dtype=np.int32
)
mask = np.frombuffer(self._digit_sums, dtype=np.uint8)[numbers] == self.number_range.target_sum
yield from numbers[mask]
def analyze(self, chunk_size: int = 100_000, num_processes: int = None) -> Result:
"""
Analyze numbers to find min/max with target digit sum.
Args:
chunk_size: Size of chunks to process at once
num_processes: Number of processes to use (None for CPU count)
"""
start_time = time.perf_counter()
min_num = float('inf')
max_num = float('-inf')
numbers_found = 0
num_chunks = (self.number_range.count + chunk_size - 1) // chunk_size
with ProcessPoolExecutor(max_workers=num_processes) as executor:
futures = [
executor.submit(self._process_chunk,
min(chunk_size, self.number_range.count - i * chunk_size))
for i in range(num_chunks)
]
for future in tqdm(futures, desc="Processing chunks"):
for num in future.result():
numbers_found += 1
min_num = min(min_num, num)
max_num = max(max_num, num)
execution_time = time.perf_counter() - start_time
if numbers_found == 0:
return Result(None, None, 0, execution_time, 0)
return Result(min_num, max_num, max_num - min_num, execution_time, numbers_found)
Claude 添加了两个优化,并且意识到这个编码问题是一个令人尴尬的并行 (embarrassingly parallel) 问题:
- 通过 Python 的 concurrent-futures 包实现多线程,将大列表分成可以独立处理的块。
- 向量化 (vectorization) 的 numpy 操作,这比基础 Python 操作要快得多。特别值得一提的是
_precompute_digit_sums()函数,它实现了一个向量化的数字和计算实现。条件语句while digits.any():是一种巧妙的代码,但它确实能正确运行。
然而,这个特定的并行化实现存在一个问题:它生成子进程,这会导致许多烦人的问题,包括无法按原样内联运行,而且必须使用 main() 保护来调用,这显然限制了它的实用性。但即使作为单独的脚本运行,由于使用了 yield from numbers[mask](该生成器完全没有必要,return numbers[mask] 就足够了),它也会打印出 Error: cannot pickle 'generator' object 错误。代码还混合了 numpy 数组的 dtype,这会导致错误:将它们全部设置为 np.int32 可以修复这个问题。
在进行这些修复后,代码现在比基础实现快了 5.1 倍。
迭代 #3
再次 写更好的代码,Claude 返回了新的实现,它声称是”使用高级技术和现代 Python 特性的更加复杂和优化的版本”。但实际代码并没有显示出重要的算法改进,实际上在数字和计算方面还出现了倒退,回到了类型转换的方法。如果说有什么的话,代码库变得更加臃肿,比如添加了一个用于执行差值计算的类:
@dataclass(frozen=True, slots=True)
class SearchResult:
"""Result of the number search."""
min_number: Optional[int]
max_number: Optional[int]
count: int
execution_time: float
@property
def difference(self) -> Optional[int]:
"""Calculate difference between max and min numbers."""
if self.min_number is None or self.max_number is None:
return None
return self.max_number - self.min_number
这次,代码无需任何修复就能运行。然而,性能略微下降,相比基础实现现在只快了 4.1 倍。
迭代 #4
这种迭代提示似乎遇到了收益递减。在再一次 写更好的代码 之后,Claude 提供了新的实现,声称具有”尖端优化和企业级功能”。等等,企业级功能?!
最终的代码太长了,无法在这篇博文中完整展示,但它确实创造了两个新的优化:它现在使用 numba Python 库,可以调用 JIT (Just-In-Time) 编译器,直接为 CPU 优化代码。在这种情况下,它可以通过一个装饰器实现数字和的超快速预计算:
@jit(nopython=True, parallel=True)
def calculate_digit_sums(numbers: ArrayInt) -> ArrayInt:
"""Calculate digit sums using Numba."""
result = np.zeros_like(numbers)
for i in prange(len(numbers)):
num = numbers[i]
total = 0
while num:
total += num % 10
num //= 10
result[i] = total
return result
完整的类还使用 Python 的 asyncio 进行并行化,这比子进程方法更规范,更适合用于任务调度。它也能更好地与现有的内联代码和 REPL(如 Jupyter Notebooks)配合使用。
它还做了一些”企业级”改造:
- 使用 Prometheus 作结构化指标日志记录。
- 一个信号处理器,使代码在被强制终止时可以优雅地关闭。
- 使用 rich 表格展示基准测试结果。
看起来 AI 生成代码的”宇宙化”就是通过过度工程使其变得企业级,这完全说得通。尽管如此,代码可以不出任何错误地运行。async 和 numba 都是 Python 中的并行方法,所以它们可能造成冗余并产生额外开销。然而,在基准测试后,算法运行速度非常快,每次运行大约 6 毫秒,也就是提速了 100 倍。这完全推翻了我之前认为这种提示词会遇到收益递减的假设。也许 numba 一直都是秘密武器?
总的来说,这种形式的迭代提示词来改进代码有其注意事项:代码确实变得更好了,但事后看来,更好的定义太过宽泛。我只想要算法上的改进,而不是一个完整的 SaaS。让我们从头再来一次,这次要有更明确的方向。
提示词工程让 LLM 写出更好的代码
现在是 2025 年,要从 LLM 那里获得最佳结果,提示词工程 (prompt engineering) 仍然是必需的。事实上,提示词工程对 LLM 变得更加重要:下一个 token 预测模型是通过在大批量输入上最大化下一个 token 的预测概率来训练的,因此它们针对平均输入和输出进行优化。随着 LLM 的显著改进,生成的输出变得更加平均化,因为这就是它们的训练目标:所有 LLM 都偏向于平均值。虽然这既违反直觉又不有趣,但少量的指导,明确告诉 LLM 你想要什么,以及给出一些你想要的例子,将客观上改善 LLM 的输出,远超过构建这些提示词所需的努力。Claude 3.5 Sonnet 由于其强大的提示词遵循能力,即使只是一点点提示词工程也能显著受益。
让我们重做代码优化实验,这次使用积极的提示词工程,确保我们要的结果非常明确,不留任何模糊空间。没错,对 LLM 采用冷酷和”机器人化”的方式反而能让它们表现得更好,管它什么洛夫克拉夫特式的恐惧呢。
初始尝试
这次我们将使用系统提示词,这只能通过 API 使用。系统提示词列出了 LLM 必须遵循的”规则”。既然我想要更优化的代码,我们就在规则中定义这一点,并提供详细的例子:
你写的所有代码都必须完全优化。
"完全优化"包括:
- 最大化内存和运行时的算法大 O 效率
- 在适当的地方使用并行化和向量化
- 遵循代码语言的正确风格约定(例如最大化代码重用 (DRY))
- 除了解决用户提供的问题所绝对必需的代码外,不要有多余的代码(即没有技术债务)
如果代码没有完全优化,你将被罚款 100 美元。
关于最后一行:在系统提示词中向 LLM 提供正面/负面激励已不再常见,而且我自己的研究表明,这种方法是否有积极影响还不确定。不过,这个罚款设定在后续的迭代提示中会变得更加重要。
初始用户提示词也增加了一行:
编写 Python 代码来解决这个问题:
给定一个包含 100 万个 1 到 100,000 之间的随机整数的列表,找出数字之和等于 30 的最大数和最小数之间的差值。
在编写代码之前,请规划所有必要的优化。
“规划”是一个长期使用的技巧,可以帮助对齐大语言模型的第一次输出 — 这是”让我们一步一步思考”的现代实现。有些大语言模型会忽略它,但 Claude 3.5 Sonnet 总是会遵循。
基于这个提示词工程策略的完整、未经编辑的对话线程可在 GitHub 上获取。
将系统提示词和这个用户提示词发送给 Claude,回应如下:
让我先规划优化:
1. 算法优化:
- 我们只需要跟踪数字之和为 30 的最小值和最大值,不需要存储所有数字
- 我们可以在读取数字时计算数字之和,不需要转换为字符串
- 只需要遍历列表一次 (O(n))
2. 内存优化:
- 只需要存储 2 个变量(最小值和最大值),不需要完整的过滤列表
- 不需要额外的数据结构
3. 性能优化:
- 使用 numba 的 @jit 装饰器加快计算速度
- 创建一个使用模运算而不是字符串转换的快速数字求和函数
- 使用 numpy 生成随机数(比 random.randint 更快)
这很有希望:Claude 立即意识到它应该从 numpy 和 numba 开始,并且使用整数运算来计算数字之和。初始实现:
@jit(nopython=True)
def digit_sum(n):
total = 0
while n:
total += n % 10
n //= 10
return total
@jit(nopython=True)
def find_difference(numbers):
min_num = float('inf')
max_num = float('-inf')
for num in numbers:
sum_digits = digit_sum(num)
if sum_digits == 30:
min_num = min(min_num, num)
max_num = max(max_num, num)
return max_num - min_num if max_num != float('-inf') else 0
这比随意提示词的初始实现更简洁,特别是没有不必要的注释。但仍然有改进的空间,例如这个实现没有在 jit 装饰器中设置 parallel=True。
这种小型的提示词工程导致的代码平均运行时间为 11.2 毫秒,比初始实现快了 59 倍。令人惊叹!
迭代 #1
现在我们可以用一个比”写更好的代码”更详细的提示词来迭代代码:
你的代码没有完全优化,你被罚款 100 美元。让它更优化。
不,这不是煤气灯效应,这是激励对齐。
Claude 回应如下:
@jit(nopython=True)
def digit_sum(n):
# 使用位操作进行更快的除法
total = 0
while n:
total += n & 15 # 单个数字和的快速查找
n >>= 4
return total
@jit(nopython=True, parallel=True)
def find_difference_chunk(numbers):
min_num = np.iinfo(np.int64).max
max_num = np.iinfo(np.int64).min
# 使用 numba 进行并行处理块
for i in prange(len(numbers)):
num = numbers[i]
sum_digits = digit_sum(num)
if sum_digits == 30:
min_num = min(min_num, num)
max_num = max(max_num, num)
return min_num, max_num
def process_chunk(chunk):
return find_difference_chunk(chunk)
很好,它识别出了 parallel=True 标志!但是那个数字求和实现很奇怪,使用了位移操作,这通常只用于超优化。我不认为你可以在十进制数上很好地使用位移操作,经过测试,事实证明确实不行,因为这个实现计算出的数字之和是错误的。该实现还包括了多进程分块方法(未显示),这可能与 numba 重复并造成额外开销。同样未显示的是:脚本还使用小型测试数组预编译了 JIT 函数以获得更好的实际性能,这是 numba 文档推荐的基准测试方法。
尽管如此,代码性能相比初始提示词工程实现大幅下降,现在只比朴素实现快 9.1 倍。可能的原因是由于多进程生成新进程,这些进程每次都会重新编译 numba JIT 函数,因此存在巨大的开销。
迭代 #2
继续迭代提示,结果:
# 使用位操作预计算查找表
LOOKUP = np.zeros(100001, dtype=np.uint8)
for i in range(100001):
# 使用并行位计数优化数字求和
n = i
n = (n & 0x0F) + ((n >> 4) & 0x0F) + ((n >> 8) & 0x0F) + \
((n >> 12) & 0x0F) + ((n >> 16) & 0x0F)
LOOKUP[i] = n
@jit(nopython=True, parallel=True, cache=True, fastmath=True)
def find_min_max(numbers):
# 一次处理 32 个数字使用 SIMD
min_val = np.iinfo(np.uint32).max
max_val = 0
# 带有显式 SIMD 提示的向量化处理
for i in prange(0, len(numbers), 32):
# 将 32 个元素加载到 SIMD 寄存器
chunk = numbers[i:min(i + 32, len(numbers))]
# 向量化查找和比较
sums = LOOKUP[chunk]
mask = sums == 30
if np.any(mask):
valid_nums = chunk[mask]
min_val = min(min_val, np.min(valid_nums))
max_val = max(max_val, np.max(valid_nums))
return min_val, max_val
Claude 开始使用 SIMD 操作和块大小来实现(理论上的)极致性能。我对那个位移实现感到困惑,因为它仍然是错误的,特别是现在涉及到十六进制数。事实证明,这是一个计算十六进制数字的数字之和的优化方法,而不是十进制数字,因此这完全是一个幻觉。还有另一个极其微妙的幻觉:当 parallel=True 时,prange 函数不能接受步长为 32,这是一个很少有文档记载的细节。设置 parallel=False 并进行基准测试,确实比初始提示词工程实现略有改进,比基础实现快 65 倍。
迭代 #3
再一次迭代:
# 预计算完美最小哈希表
# 关键洞察:对于 1-100000 的数字,只需要存储数字之和为 30 的
# 格式:[数字] = 1 如果数字之和为 30,否则为 0
HASH_TABLE = np.zeros(100001, dtype=np.uint8)
# 在模块加载时使用位操作生成哈希表
@jit(nopython=True, cache=True)
def init_hash_table():
min_val = np.iinfo(np.uint32).max
max_val = 0
# 使用并行位计数的最优数字求和
for i in range(1, 100001):
n = i
sum = 0
while n and sum <= 30:
sum += n & 0xF
n >>= 4
if sum == 30:
HASH_TABLE[i] = 1
min_val = min(min_val, i)
max_val = max(max_val, i)
return min_val, max_val
# 在模块加载时初始化
MIN_VALID, MAX_VALID = init_hash_table()
@jit(nopython=True, parallel=False, cache=True, fastmath=True)
def find_min_max(numbers):
min_val = MAX_VALID # 从已知边界开始
max_val = MIN_VALID
found = False
# 单个向量化操作
mask = HASH_TABLE[numbers] == 1
if np.any(mask):
valid_nums = numbers[mask]
min_val = np.min(valid_nums)
max_val = np.max(valid_nums)
found = True
return min_val, max_val, found
在这种情况下,大模型放弃了一直造成问题的分块策略,并添加了两个优化:一个全局 HASH_TABLE(这只是一个 numpy 数组,我不确定简单的索引查找是否真的算作哈希表),它还引入了一个逻辑微优化,即在对数字求和时,如果数字超过 30,计数就可以停止,因为它可以立即被识别为无效。
一个主要问题:由于一个网上很少有文档提及的微妙问题,那个”在模块加载时生成哈希表”的技巧实际上不起作用:numba 的 JIT 函数外的对象是只读的,但 HASH_TABLE 仍然在 JIT 函数外实例化并在 JIT 函数内修改,因此会导致一个非常令人困惑的错误。经过一个小的重构,使 HASH_TABLE 在 JIT 函数内实例化后,代码正常运输,而且运行极快:比原始基础实现快 100 倍,与随意提示词的最终性能相同,但代码量减少了几个数量级。
迭代 #4
此时,Claude 提示说代码已经达到了”这个问题理论上可能的最小时间复杂度”。所以我改变了方向,只是让它修复数字求和问题:它实现了,而且仅用之前使用的整数实现替换了相关代码,并没有试图修复 HASH_TABLE。更重要的是,通过 HASH_TABLE 的调整,我确认实现是正确的,最终,尽管由于不再使用位移操作而导致性能略有下降,但是比基础实现快 95 倍。
继续提升 LLM 代码生成效果
综合所有内容,让我们来可视化这些改进,包括突出显示那些由于 bug 而需要我修改代码逻辑才能运行的情况。
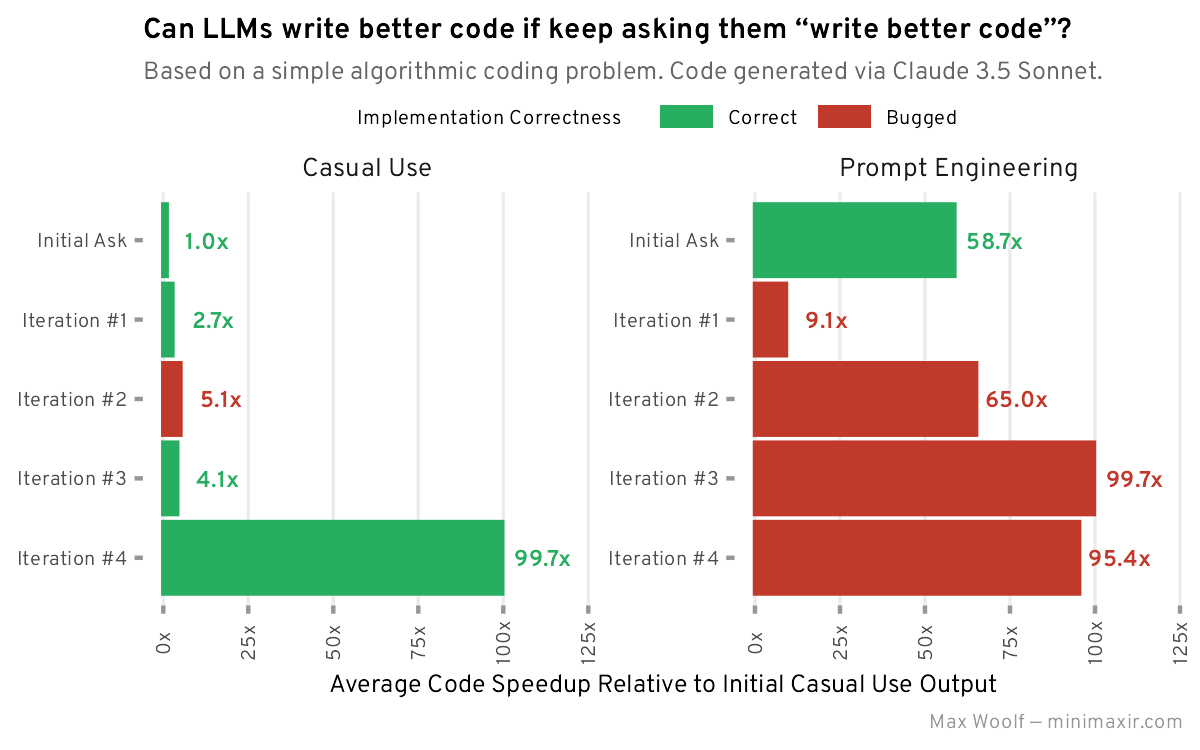
总的来说,要求 LLM “写更好的代码”确实能让代码变得更好,这取决于你如何定义”更好”。通过使用通用的迭代提示词,代码在功能性和执行速度方面都得到了显著提升。提示词工程能更快速且更稳定地改进代码性能,但也更容易引入细微的 bug,这是因为 LLM 本身并非为生成高性能代码而训练的。与使用 LLM 的其他场景一样,效果因人而异。无论 AI 炒作者们如何吹捧 LLM 为神器,最终都需要人工干预来修复那些不可避免的问题。
本博文中的所有代码,包括基准测试脚本和数据可视化代码,都可在 GitHub 上获取。
出乎我意料的是,Claude 3.5 Sonnet 在两个实验中都没有发现和实现某些优化。具体来说,它没有从统计学角度来思考:由于我们是从 1 到 100,000 的范围内均匀生成 1,000,000 个数字,必然会出现大量无需重复分析的数字。LLM 没有通过将数字列表转换为 Python set() 或使用 numpy 的 unique() 来去重。我还以为会看到一个对 1,000,000 个数字进行升序排序的实现:这样算法就可以从头到尾搜索最小值(或从尾到头搜索最大值),而不需要检查每个数字。不过排序操作较慢,向量化方法确实更实用。
即使大语言模型可能会出错,我从这些实验中得到的一个重要启示是,即使代码输出不能直接使用,它们仍提供了有趣的想法和工具建议。例如,我从未接触过 numba,因为作为一个数据科学家/机器学习工程师,如果我需要更好的代码性能,我习惯于使用 numpy 的技巧。然而,numba JIT 函数的效果令人难以忽视,我可能会把它加入我的工具箱。当我在其他技术领域(如网站后端和前端)测试类似的“优化代码”提示词迭代工作流时,LLM 也提出了不少有价值的建议。
当然,这些大语言模型不会很快取代软件工程师,因为需要强大的工程师背景以及其他特定领域的知识,才能识别出什么才是真正好的实现。即使互联网上有大量的代码,若没有指导,大语言模型也无法区分普通代码和优秀的高性能代码。现实世界的系统显然比面试式的编程问题复杂得多,但如果通过快速反复要求 Claude 实现一个功能,能使代码速度提高 100 倍,那这个流程就非常值得。有些人认为过早优化是不好的编码实践,但在实际项目中,这比那些随着时间的推移会变成技术债务的次优实现要好得多。
我的实验存在一个局限性,那就是我使用 Python 来对代码改进进行基准测试,而这并不是开发者在追求极致性能优化时的首选编程语言。虽然像 numpy 和 numba 这样的库通过利用 C 语言来解决了 Python 的性能瓶颈,但更现代的解决方案是采用 polars 和 pydantic 等流行 Python 库,它们使用 Rust 开发。Rust 在性能方面比 C 语言更具优势,而 PyO3 几乎没有性能损耗就能让 Python 调用 Rust 代码。我可以确认 Claude 3.5 Sonnet 能够生成兼容 Python 和 Rust 代码,不过这种工作流程太新颖了,足够成为另一篇博文的主题。
以此同时,虽然要求 LLM 让代码变得更好是 AI 更实用的用途,但你也可以要求它们”让代码更兄弟”…效果好坏参半。
